Proximity induced superconductivity in a normal conductor is a rich field of experimental and theoretical investigations in many systems. In the last decade, it has been particularly at the heart of the quest for realizing topological modes in hybrid superconductor-nanowire nanodevices. Yet, and very surprisingly, it turns out that there was a clear lack of investigations in simple systems which should have been done before turning to more complex hybrid devices. This is precisely what is done in this work where an ultra-clean carbon nanotube (CNT) coupled to a superconducting lead is investigated, a system that cannot host topological modes by design.
We observed for the first time a long standing prediction of random matrix theory (RMT), dating back to 2001, that mesoscopic fluctuations of the mini-gap in a conductor follow a universal distribution. Interestingly, mesoscopic fluctuations of the minigap were precisely to lead to ubiquitous nontopological edge states clustering towards zero energy. We indeed observed ubiquitous and robust zero bias conductance peaks in our device. This result goes beyond recent experimental investigations of nontopological states in proximity induced semiconducting nanowire devices as the semiconducting nanowire used in these works had a strong intrinsic spin-orbit interaction and its role cannot be ruled out in explaining the observed zero bias conductance peaks. Instead our CNT shows a weak spin-orbit interaction. But more importantly, the RMT predictions that we confirm are very general and must be present in any system showing disorder, even if it is weak. This work thus provides the first real benchmark of a superconductor-nanowire device in an elemental situation.
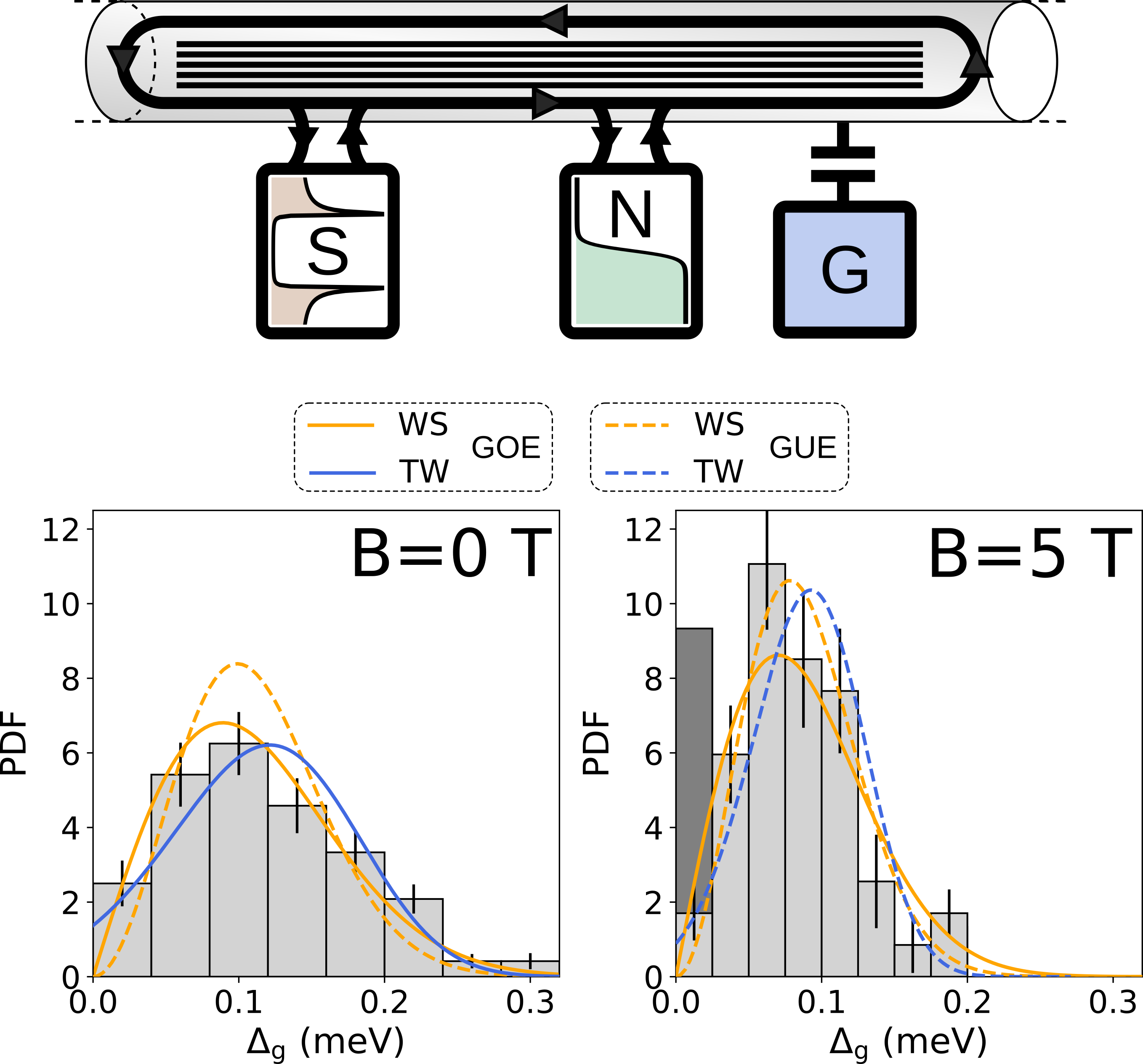
(Top) Illustration of the device showing the nanowire with small level spacing contacted to a normal reservoir (green) and to a superconducting reservoir (brown). The gate electrode (blue) is capacitively coupled to the nanowire. (Bottom) Normalized histograms of the mini-gap for B=0T and B=5T. The bar height is the value of the probability density function (PDF) at the bin, normalized such that the integral over the range is 1. Curves are PDF of Wigner surmise (WS) in orange and Tracy-Widom (TW) in blue, with solid lines for Gaussian orthogonal ensemble (GOE) and dashed lines for Gaussian unitary ensemble (GUE).
More:
https://www.nature.com/articles/s41467-022-33960-z
Affiliation author:
Laboratoire de physique de L’École normale supérieure (LPENS, ENS Paris/CNRS/Sorbonne Université/Université de Paris)
Corresponding author: Matthieu Delbecq
Communication contact: L’équipe de communication